Calculating beam load is one of the cornerstones of structural design. Whether you’re an aspiring engineer or an experienced architect, understanding how to calculate beam load ensures that your structure is both safe and cost-effective.
A beam acts as a backbone of many structures—bridges, buildings, and even furniture. It’s the element that carries loads from above and transfers them to supports below.
In this comprehensive guide, we’ll explore the entire process — from understanding loads to performing calculations manually and using professional software tools. Let’s dive into the world of structural precision.
Understanding What a Beam Load Is
A beam load refers to the total force applied to a beam, whether it’s from walls, floors, or environmental factors like snow or wind. When these forces act on a beam, they create bending moments, shear forces, and deflections.
In simple terms:
A beam load is the total weight or force a beam must carry without bending, cracking, or failing.
Beam load calculations help determine:
- The size of the beam
- The type of material (steel, concrete, timber)
- The support requirements
- The maximum load capacity
Understanding this concept ensures that engineers can design structures that last for decades without compromise.
Types of Loads Acting on Beams
Beams encounter various types of loads during their lifespan. Let’s break them down:
1. Dead Load
- Permanent or static load.
- Includes beam self-weight, flooring, walls, and fixed installations.
2. Live Load
- Temporary or movable loads.
- Includes people, furniture, and vehicles.
3. Point Load
- Concentrated load acting at a single point.
- Common in machinery support or column resting.
4. Uniformly Distributed Load (UDL)
- Evenly spread load across the beam’s length.
- Common in floors and slabs.
5. Varying Load
- Intensity changes along the beam.
- Example: wind pressure or triangular load.
Each type of load affects bending and shear differently, so knowing what type you’re dealing with is essential for accurate calculations.
Types of Beams Used in Structures
Beams are categorized based on how they’re supported and the way they transfer loads.
| Type of Beam | Description | Common Usage |
|---|---|---|
| Simply Supported | Supported at both ends | Residential floors, small bridges |
| Cantilever | Fixed at one end, free at the other | Balconies, overhangs |
| Fixed | Both ends fixed | Frames, heavy load structures |
| Continuous | More than two supports | Multi-span floors |
| Overhanging | Extends beyond its support | Canopies, shade structures |
Each beam type demands a different calculation approach. For instance, a cantilever beam experiences maximum moment at the fixed end, while a simply supported beam does so at the midspan.
Fundamental Terms in Beam Load Analysis
Before calculating, you should understand these core concepts:
Reaction Forces
Forces at the supports that balance external loads.
Shear Force (V)
The internal resistance to sliding forces within the beam.
Bending Moment (M)
The turning effect caused by loads that lead to bending.
Deflection (δ)
The vertical displacement of a beam due to applied loads.
Understanding these terms helps you interpret shear force diagrams (SFDs) and bending moment diagrams (BMDs) accurately.
Essential Formulas for Beam Load Calculation
Beam load calculations rely on standard equations that help engineers determine support reactions, shear forces, and bending moments for various loading conditions.
Below is a summary of the most important beam load formulas used in structural analysis and design.
🧮 Beam Load Calculation Formulas Table
| Type of Beam & Loading | Reaction Formula | Maximum Bending Moment Formula | Remarks |
|---|---|---|---|
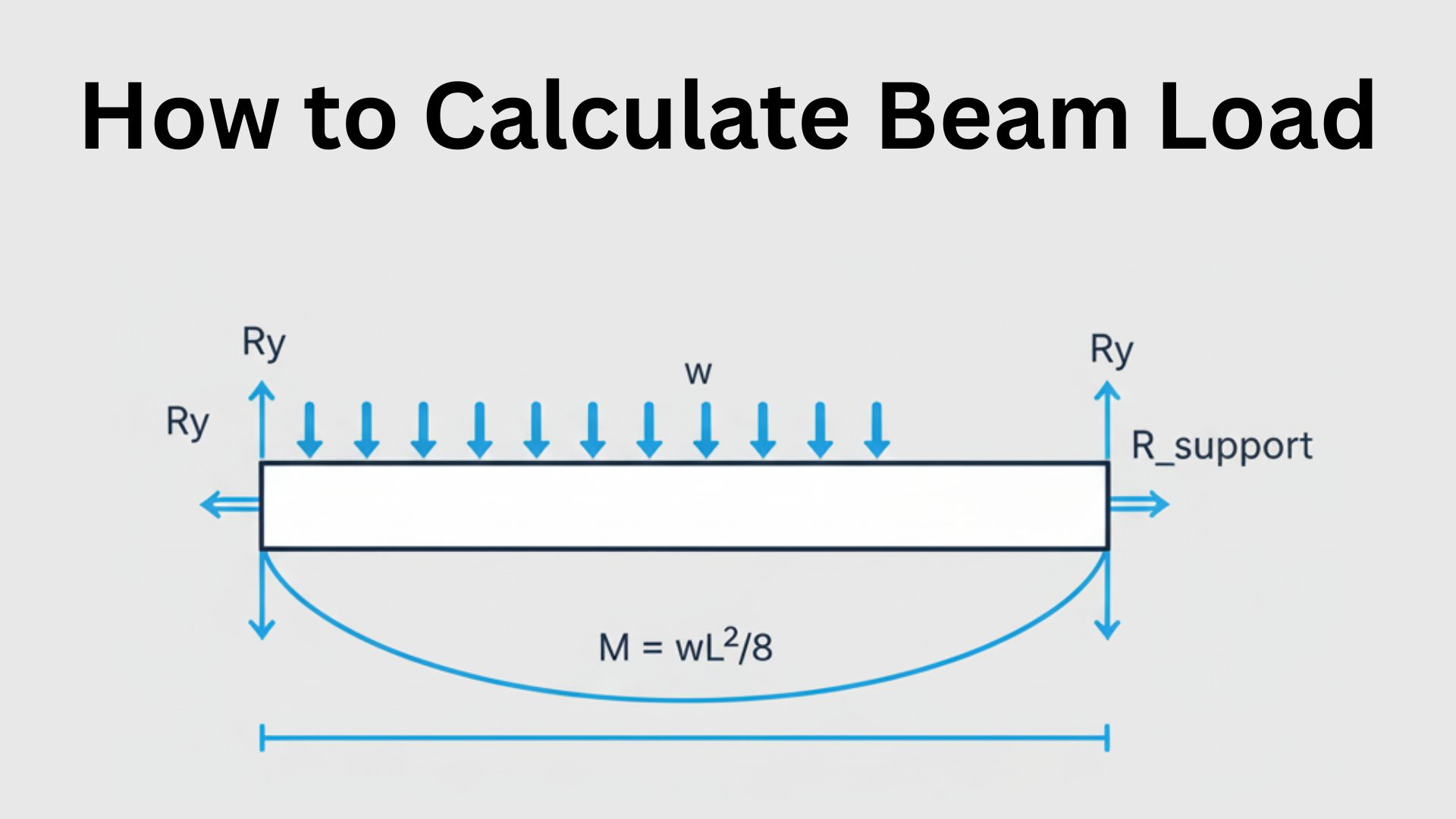
| 1. Simply Supported Beam with Uniformly Distributed Load (UDL) | RA=RB=wL2R_A = R_B = \dfrac{wL}{2}RA=RB=2wL | Mmax=wL28M_{max} = \dfrac{wL^2}{8}Mmax=8wL2 | Maximum moment occurs at midspan. |
| 2. Cantilever Beam with Uniformly Distributed Load (UDL) | R=wLR = wLR=wL | Mmax=wL22M_{max} = \dfrac{wL^2}{2}Mmax=2wL2 | Maximum moment at the fixed end. |
| 3. Simply Supported Beam with Central Point Load | RA=RB=P2R_A = R_B = \dfrac{P}{2}RA=RB=2P | Mmax=PL4M_{max} = \dfrac{PL}{4}Mmax=4PL | Maximum moment at the beam’s center. |
| 4. Cantilever Beam with Point Load at Free End | R=PR = PR=P | Mmax=PLM_{max} = PLMmax=PL | Moment acts at the fixed support. |
| 5. Fixed Beam with Uniformly Distributed Load | RA=RB=wL2R_A = R_B = \dfrac{wL}{2}RA=RB=2wL | Mmax=wL212M_{max} = \dfrac{wL^2}{12}Mmax=12wL2 | Smaller moment compared to simply supported beam. |
Essential Formulas for Beam Load Calculation
Beam load calculations rely on standard equations that help engineers determine support reactions, shear forces, and bending moments for various loading conditions. Below is a summary of the most important beam load formulas used in structural analysis and design.
| Type of Beam & Loading | Reaction Formula | Maximum Bending Moment Formula | Remarks |
|---|---|---|---|
| 1. Simply Supported Beam with Uniformly Distributed Load (UDL) | RA = RB = wL / 2 | Mmax = wL2 / 8 | Maximum moment occurs at midspan. |
| 2. Cantilever Beam with Uniformly Distributed Load (UDL) | R = wL | Mmax = wL2 / 2 | Maximum moment at the fixed end. |
| 3. Simply Supported Beam with Central Point Load | RA = RB = P / 2 | Mmax = P × L / 4 | Maximum moment at the beam’s center. |
| 4. Cantilever Beam with Point Load at Free End | R = P | Mmax = P × L | Moment acts at the fixed support. |
| 5. Fixed Beam with Uniformly Distributed Load (UDL) | RA = RB = wL / 2 | Mmax = wL2 / 12 | Smaller moment compared to a simply supported beam. |
Explanation of Symbols
- RA, RB: Reactions at supports
- R: Reaction at fixed support
- w: Uniformly distributed load (kN/m)
- L: Span or length of the beam (m)
- P: Point load (kN)
- Mmax: Maximum bending moment (kNm)
These fundamental beam load formulas serve as the basis of structural design. They allow engineers to perform quick manual calculations, preliminary sizing, and verification of results from structural analysis software.
📘 Explanation of Symbols
- RA,RBR_A, R_BRA,RB: Reactions at supports
- RRR: Reaction at fixed support
- www: Uniformly distributed load (kN/m)
- LLL: Span or length of the beam (m)
- PPP: Point load (kN)
- MmaxM_{max}Mmax: Maximum bending moment (kNm)
These fundamental beam load formulas serve as the basis of structural design.
They allow engineers to make quick calculations for manual checks, preliminary sizing, and validation of results from advanced analysis software.
10-Step Method: How to Calculate Beam Load Accurately
Follow these expert steps for reliable calculations:
Step 1: Identify the beam type (simply supported, cantilever, etc.)
Step 2: Determine the type of load (UDL, point, varying).
Step 3: Compute total load on the beam:
Total Load=w×L\text{Total Load} = w \times LTotal Load=w×L
Step 4: Calculate reactions using equilibrium equations.
Step 5: Draw shear force diagram (SFD).
Step 6: Draw bending moment diagram (BMD).
Step 7: Locate maximum bending moment.
Step 8: Check for deflection using:
δ=5wL4384EI\delta = \frac{5wL^4}{384EI}δ=384EI5wL4
Step 9: Compare with allowable deflection limits.
Step 10: Verify design safety and material capacity.
Worked Example: Full Beam Load Calculation
Given:
- Simply supported beam
- Span = 6 m
- UDL = 10 kN/m
Step 1: Reactions RA=RB=10×62=30 kNR_A = R_B = \frac{10 \times 6}{2} = 30 \text{ kN}RA=RB=210×6=30 kN
Step 2: Maximum Moment Mmax=10×628=45 kNmM_{max} = \frac{10 \times 6^2}{8} = 45 \text{ kNm}Mmax=810×62=45 kNm
Step 3: Shear Force Vmax=30 kNV_{max} = 30 \text{ kN}Vmax=30 kN
Step 4: Deflection δ=5(10×103)(6000)4384(200,000)(1.5×108)=7 mm (approx.)\delta = \frac{5(10 \times 10^3)(6000)^4}{384(200,000)(1.5 \times 10^8)} = 7 \text{ mm (approx.)}δ=384(200,000)(1.5×108)5(10×103)(6000)4=7 mm (approx.)
Result:
Beam is safe and within deflection limits.
Common Mistakes to Avoid
- Ignoring beam’s self-weight
- Mixing units (e.g., N and kN)
- Misidentifying load type
- Forgetting safety factors
- Using wrong support assumptions
Being precise in every calculation step ensures reliable and safe designs.
Beam Load Calculation Tools & Software
Here are trusted tools professionals use:
- STAAD.Pro – Advanced 3D structural analysis.
- ETABS – For multistory building analysis.
- SAP2000 – Great for frames and bridges.
- SkyCiv Beam Calculator – Free, web-based tool.
- Autodesk Robot Structural Analysis – For detailed simulation.
External Link:
Check SkyCiv’s Online Beam Calculator for quick analysis.
Tips for Accurate Structural Calculations
- Always add beam self-weight.
- Use consistent units.
- Follow local design codes (IS 875, ASCE 7, Eurocode).
- Cross-check results using software.
- Apply a safety factor for uncertain loads.
Real-World Applications of Beam Load Analysis
- Bridge construction – to determine load-bearing capacity.
- Building design – for slab and column load transfer.
- Industrial setups – machinery and crane beam design.
- Architectural elements – canopies, balconies, and decks.
Accurate load calculations ensure long-term performance and public safety.
FAQs About Beam Load Calculations
1. Why is calculating beam load important?
It ensures that structures are safe, durable, and cost-efficient.
2. What units are used in beam calculations?
Loads in kN, length in m, and moments in kNm.
3. Can I calculate beam load manually?
Yes, by applying equilibrium equations and basic structural formulas.
4. What’s the difference between dead and live load?
Dead loads are permanent; live loads are temporary or movable.
5. What happens if beam load exceeds design capacity?
It leads to excessive deflection, cracking, or even collapse.
6. How do I include self-weight?
Multiply the beam’s cross-section area by its material density and gravity.
Conclusion
Mastering how to calculate beam load is vital for any engineer or architect who values precision and safety.
By understanding load types, applying the right formulas, and checking for deflection, you ensure structural integrity. Whether using manual methods or advanced software, beam load calculation is the foundation of safe, efficient, and reliable structural design.